TRIáNGULOS Y CUADRILATEROS

Triángulo: Es la figura geométrica formada por tres puntos no alineados y por tres segmentos que los unen.

Los triángulos los podemos clasificar de dos formas:

1. Según sus ángulos:

Rectángulo: Es el triángulo que tiene un ángulo recto 90º.

Obtusángulo: Es aquel que tiene un ángulo obtuso  > de 90º  y  <  de  180º.

Acutángulo: Cuando sus tres ángulos son agudos < de 90º.

2. Según sus lados:

Equilátero: Es el triángulo que tiene sus tres lados iguales (congruentes).

Isósceles: Es el que tiene dos lados iguales y uno desigual.

Escaleno: Es el triángulo que tiene sus tres lados desiguales.

LíNEAS Y PUNTOS DEL TRIáNGULO

BISECTRíZ: Geométricamente es una línea que divide una superficie en dos partes iguales.

Explicación: Se han localizado dos puntos  Q y R  sobre los lados adyacentes del vértice  C,  (lados  CA y CB) a una misma distancia del vértice  C. Luego tomamos el compás y haciendo centro en cada uno de los puntos  Q y R, con una abertura mayor al vértice C, trazamos los arcos respectivos y marcamos el punto de intersección F. Luego trazamos una recta desde el vértice C que pase por el punto F. A ésta línea la llamamos bisectriz,  CF.

Para cada vértice realizamos el mismo procedimiento y nos podemos dar cuenta que un triángulo posee tres bisectrices que se cortan en un punto común. éste punto recibe el nombre de  INCENTRO.

ALTURA: Es la recta que une cualquier vértice con el lado opuesto o su prolongación en forma perpendicular. Todo triángulo posee tres alturas que se cortan en un punto común, que recibe el nombre de  ORTOCENTRO.

MEDIANA: Es la línea  recta que une cualquiera de los tres vértices del triángulo, con el punto medio del lado opuesto de cada uno de los tres vértices.

El punto de corte de las tres medianas recibe el nombre de  BARICENTRO. Todo triángulo tiene tres medianas.

MEDIATRIZ: Es la línea perpendicular trazada por el punto medio de cualquiera de los tres lados de un triángulo. Los triángulos poseen también tres mediatrices que coinciden en un punto común, que llamamos  CIRCUNCENTRO.

Para trazar una perpendicular a cualquiera de los lados de un triángulo colocamos una escuadra sobre el lado con el extremo o punta del ángulo de 90º sobre el punto medio previamente marcado, y trazamos la recta  hacia el interior del triángulo.

CUADRILáTEROS

Cuadrilátero:   es la figura geométrica que tiene cuatro lados. Hay varias clases de cuadriláteros, los más importantes son:

Rectángulo: es al figura geométrica que tiene sus lados iguales y paralelos de dos en dos, además sus cuatro ángulos son rectos, 90º. Pero dos de sus lados son diferentes a los otros dos.

Paralelogramo: es la figura geométrica que tiene sus lados iguales y paralelos de dos en dos, pero tiene sus ángulos internos diferentes a 90º.

Cuadrado: es al figura geométrica que tiene todos sus lados iguales y son paralelos de dos en dos, además tiene sus cuatro ángulos internos iguales a 90º.

Rombo: figura geométrica que tiene sus lados iguales y paralelos de dos en dos, pero sus ángulos internos pueden ser diferentes de 90º, además una de sus diagonales es diferente a la otra.

  a = b = c = d

 CD  >  AB

ángulos internos

 diferentes de 90º

Las anteriores figuras geométricas también reciben el nombre general de  POLíGONOS, y se amplía la variedad dependiendo del número de sus lados.

POLíGONO: figura geométrica formada por la unión de varios segmentos(lados) sabiendo que se unen sólo en los extremos.

La suma de las medidas de los ángulos internos de un polígono es igual al número de los lados menos dos por 180º, es decir  ( n - 2) x 180º donde  n  es el número de lados del polígono.

Así para hallar la suma de las medidas de los ángulos internos de un hexágono, decimos:

Hexágono  =  6 lados

( n ¯ 2) x 180º  =  (6 - 2) x 180º  =  4 x 180º  =  720º

Los polígonos que tienen ángulos internos que sumen menos de 180º reciben el nombre de convexos, y cuando por lo menos uno de sus ángulos internos miden más de 180º recibe el nombre de cóncavo.

Un polígono es regular cuando todos sus lados son iguales, por ejemplo el cuadrado, y es Irregular cuando por lo menos uno de sus lados tiene diferente longitud que los demás, por ejemplo el triángulo escaleno.

PERíMETRO Y áREA

Perímetro: es la medida de un contorno.

área: es la parte de una superficie ó extensión.

Ejemplo:

Hallar el área de la siguiente figura:

áREAS DE FIGURAS GEOMéTRICAS

CIRCUNFERENCIA

Es una curva plana cerrada, cuyos puntos equidistan de otro llamado centro. Considerando la circunferencia como base podemos establecer varias posiciones de una recta:

La recta  AB  se llama externa porque no tiene ningún punto en común con la circunferencia.

La recta  CD  es tangente a la circunferencia porque posee un punto en común con ésta.

La recta  EF  la llamamos secante, porque posee y corta a la circunferencia en mas de un punto.

En la circunferencia encontramos otro tipo de líneas importantes y con características especiales:

Cuerda: es un segmento de recta que une a dos puntos de la circunferencia, representado por el segmento  AB.

Diámetro: es la cuerda mayor de la circunferencia que une a dos puntos, con la característica que pasa por el centro d la circunferencia. Lo representamos por el segmento  EF.

Radio: segmento de recta que une al centro de la circunferencia con cualquier otro punto de ésta. Segmento  OJ.

semicircunferencia: es el segmento de curva que equivale a la mitad de la circunferencia.

Arco: es la  porción de la circunferencia  limitado por los puntos AB.

TRASLACIóN

Este concepto  hace parte de la geometría de desplazamiento. La traslación de un cuerpo la definimos como el efecto de trasladar ó cambiar de lugar un cuerpo, pero sobre un mismo plano y con movimiento recto.

Podemos  realizar  una traslación consecutiva de  un cuerpo geométrico, en un plano cartesiano, indicando  la dirección (derecha ó izquierda) y la magnitud (unidades) respecto de un eje de coordenadas.

Realicemos una traslación de un objeto, hacia la derecha y paralelo al eje de las x, luego hacia abajo paralelo al eje de las y. La traslación sería:

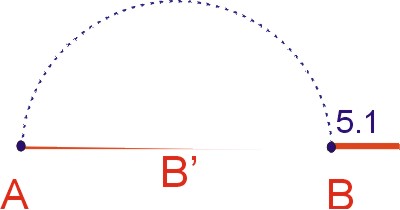
Sea el segmento  AB, trazado en el plano cartesiano, lo hemos girado 90º en dirección de las manecillas del reloj. La trayectoria es una línea curva representando el giro por una serie de puntos, el punto B gira 90º y toma coordenadas (5, 1)  sobre el eje  x al cual lo representamos como  B´. El eje ó centro de rotación  del giro ha sido el punto A.