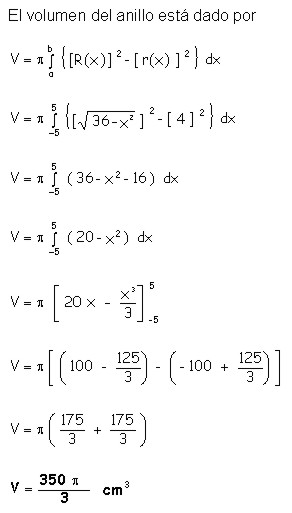UNIDAD 4
4.1 Integración
La integración es la operación inversa de la derivada, y uno de Los objetivos de esta unidad es el que el usuario analice, reconozca y aplique los conceptos de la antiderivada y diferencie cuando una función es antiderivada de otra.
El usuario logrará deducir las propiedades de una integral definida, así como conceptualizar y definir las propiedades de sumatoria. En general se busca una aplicación de los conceptos fundamentales de la integración a los diferentes problemas de cálculo, de integrales y áreas localizadas por debajo de una función.
4.1.2 Antiderivada e integración
indefinida 

Podemos observar que las antiderivadas de una misma función se diferencian en el valor de la constante. Entonces, se puede hallar ahora la antiderivada de una forma más general de una función dada.
Ejemplo:

La función f(x) es el integrando y dx es el diferencial de x. El número o la constante C es la constante de integración.
El concepto de integral definida lo desarrollaremos mediante el análisis de algunos ejemplos. La verificación de una integral indefinida se trata de observar que el integrando sea igual a la derivación del resultado obtenido, es decir:
Evaluar las siguientes integrales indefinidas:

De los anteriores ejemplos se puede definir dos de las reglas básicas de integración:

y se define otra propiedad fundamental:
![]()
Otras reglas básicas de integración y su respectiva comparación con las fórmulas de derivación se pueden resumir en la siguiente gráfica:
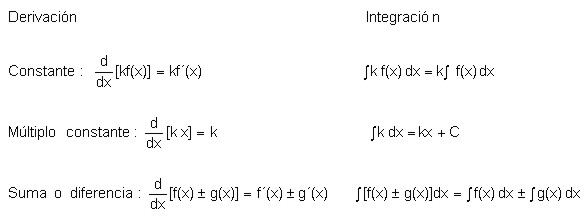
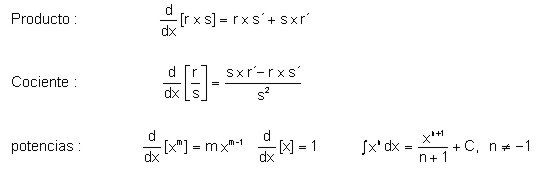
Funciones Trigonométricas:

Ejemplo:
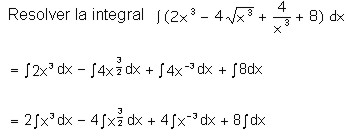

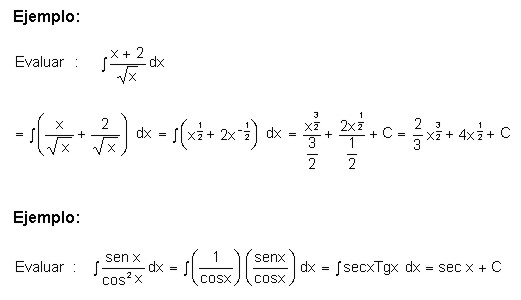
4.1.4 Integración por sustitución

La integración por sustitución es otra aplicación de la regla de la cadena en funciones compuestas. Recordemos el concepto básico de la regla de la cadena vista en la unidad tres del presente curso:

De la anterior definición se deduce para la integración:
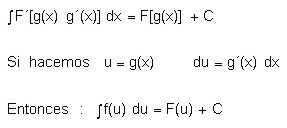
Ejemplo:

Ejemplo:



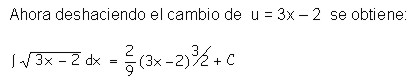
Ejemplo:


A la variable k se le denomina índice sumatorio e indica el valor que toma la constante k inicialmente. Al ir aumentando el valor de la constante de uno en uno, se debe llegar hasta el valor final que aparece en la parte superior del símbolo de la sumatoria.
Ejemplos:
Evaluar las siguientes sumatorias:
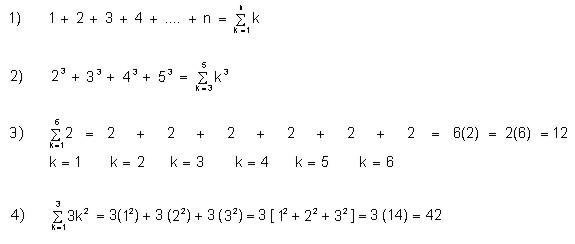
4.1.5.1 Propiedades de la sumatorias

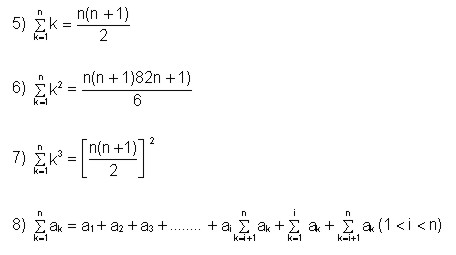
Las anteriores propiedades de las sumatorias son aplicables a la solución de hallar un área de una región en el plano. El área de la región en un plano está definida por una función f contínua y no negativa
4.1.5.2 Ejemplo de aplicación:

![]()
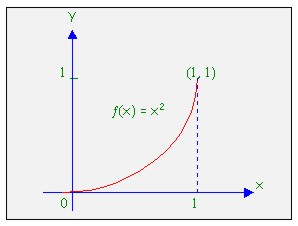
Solución:

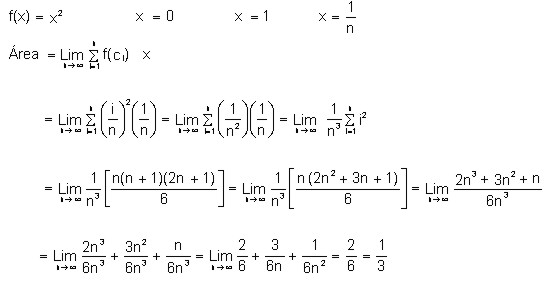
4.1.6 Integral definida y suma
de Riemann 
El concepto de la integral definida parte de la base de tener una función f(x) definida en el intervalo cerrado [a, b], veamos lo que sucede al dividir dicho intervalo en n subintervalos:
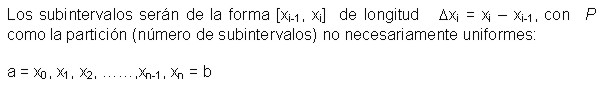
Ahora, se toma de la partición el intervalo [a, b] un subintervalo que sea el de mayor longitud y designémoslo por la letra P (norma de la partición).



Ejemplo:

Entonces definamos por conveniencia D dividiendo el intervalo [-2, 1] en n subintervalos de igual longitud:


Las integrales definidas pueden ser positivas, negativas o sin valor alguno. Para describir la integral definida como un área de una función, dicha función debe satisfacer la condición de que si es continua y no negativa en un intervalo cerrado [a, b], entonces el área de la región limitada por la función, el eje de coordenadas x y las líneas verticales x = a y x = b viene dada por:
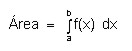
Esta fórmula es aplicable en geometría para encontrar el área de las principales figuras y cuerpos geométricos.
Ejemplos:

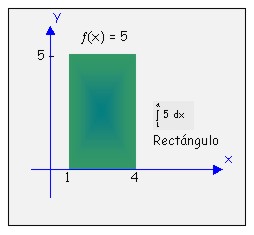
Como se puede observar la región correspondiente es un rectángulo de altura 5 y de ancho 3. Por consiguiente:
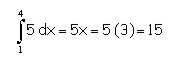
![]()
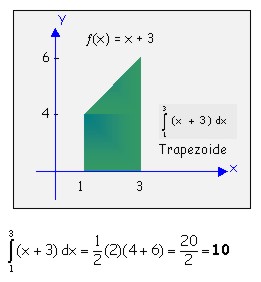
4.1.6.1 Propiedades de las integrales definidas
1. Intercambiar los límites de integración significa cambiar el signo de la integral.
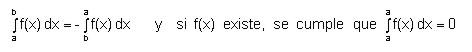
2. Si f y g son integrales en el intervalo cerrado [a, b] y k una constante, se tiene que:
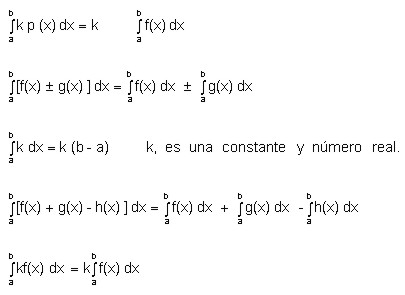
3. Si una función ¦ es integrable en tres intervalos definidos por a, b y c, se tiene que:
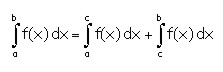
Ejemplo:
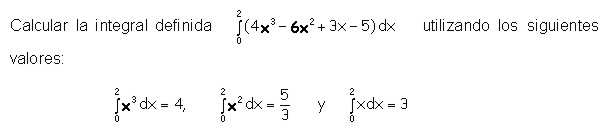

4.1.7 Teorema fundamental del
cálculo 
El teorema fundamental del cálculo, se refiere a que si una función f es continua en el intervalo cerrado [a, b], entonces la integral en el mismo intervalo cumple con la condición:
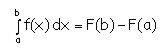
Donde F es cualquier función tal que F(x) = f(x) para todo x en el intervalo cerrado [a, b].
Ejemplos:
Evaluar las siguientes integrales definidas
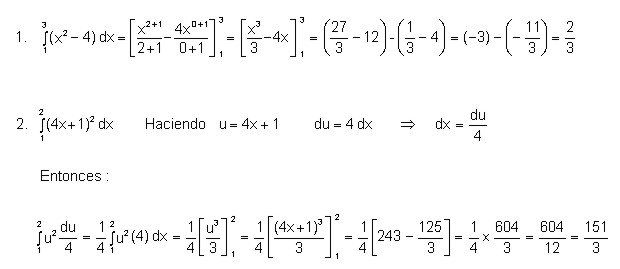
4.1.8 Sustitución de variables

Ejemplos:
Evaluar las siguientes integrales
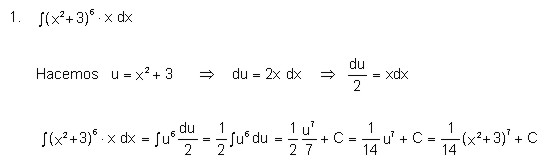
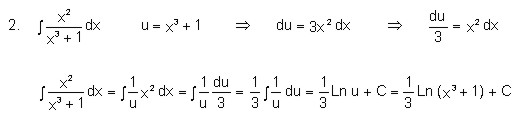
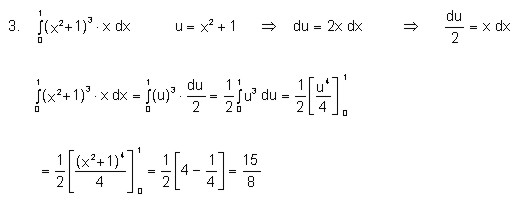
4.1.9 Cambio de los límites
de integración en una integral definida
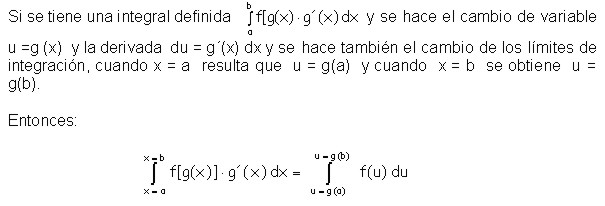
Ejemplo:
Evaluar
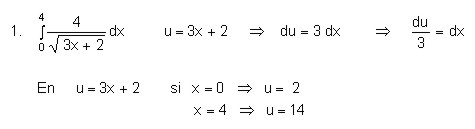

4.1.10 Valor promedio de una
integral 
El valor promedio de una función continua en un intervalo cerrado [a, b], viene dado por la fórmula:
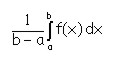
Ejemplo:
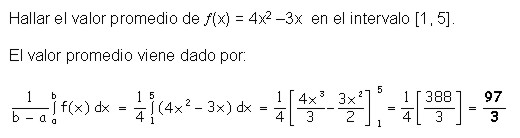
4.1.11 Función logaritmo natural

La función logaritmo natural viene dada por la expresión
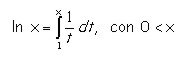
y tiene las siguientes propiedades:

Además de las anteriores propiedades del logaritmo natural también se pueden mencionar:

Ejemplo:
Calcular la derivada de la función:

4.1.12 Función exponencial
natural 

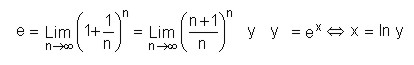
La base del logaritmo natural es e, que denota un número real positivo, de tal manera que:

Ejemplos:
Calcular las derivadas de las siguientes funciones:

Evaluar las siguientes integrales:
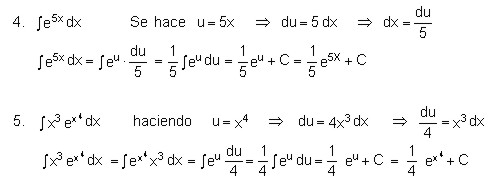
4.1.13 Función exponencial y
logarítmica en base a 
Si a es un número real positivo con la condición de que sea diferente de 1, y x un número real cualquiera entonces:
![]()
De igual manera, si a es un número real positivo con la condición de que sea diferente de 1, y x un número real positivo cualquiera entonces.
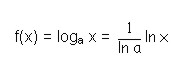
Siendo f la función logarítmica en base a. De los anteriores conceptos, se desprenden una serie de derivadas para bases diferentes de a que se pueden resumir en las siguientes:
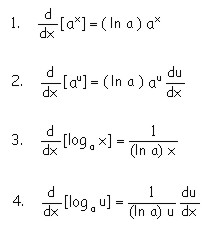
Ejemplos:
Calcular las siguientes derivadas:

4.1.14 Integrales de funciones
trigonométricas

Se demostrará algunas de las integrales de las funciones trigonométricas, las restantes se dejarán para que el usuario desarrolle las respectivas demostraciones.
Demostrar:

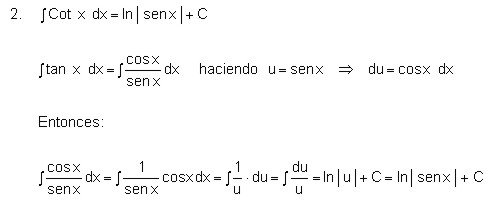

4.1.15 Derivadas de las funciones
trigonométricas inversas 
Si se tiene una función u derivable en x, entonces:

Ejemplos:
Resolver las derivadas:
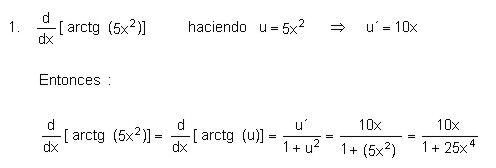
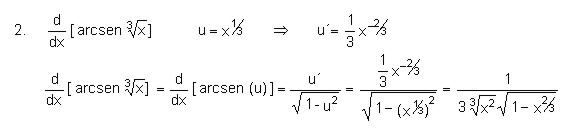
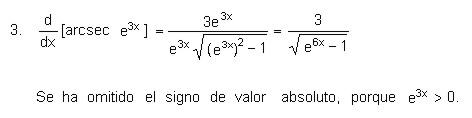
4.1.16 Integrales trigonométricas
inversas 
Siendo u una función derivable de x, se cumple que

Ejemplo:
Calcular
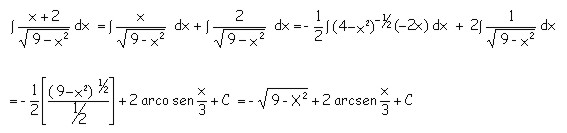
La integración por partes se fundamenta en la fórmula desarrollada para un producto, recordemos:


Ejemplos: 1.
Calcular la integral:


Del anterior procedimiento, se puede establecer una norma general para desarrollar las integrales que contienen las funciones seno y coseno:
1. Si en una integral la potencia de la función seno es positiva e impar, entonces se conserva un factor seno y se convierte los restantes factores en cosenos. Seguidamente se desarrolla e integra.

2. Si en una integral la potencia de la función coseno es positiva e impar, entonces se conserva un factor coseno y se convierte los restantes factores en senos. Seguidamente se desarrolla e integra.


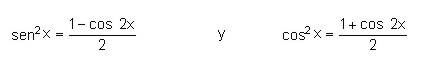
Para transformar el integrando en potencias impares del coseno.
Luego se continúa como en el caso 2.





4.1.18 Área de una región entre
dos curvas 
El área de una región entre dos curvas es una de las aplicaciones más importantes de la integral definida y se enuncia de acuerdo a la siguiente consideración

Ejemplos:

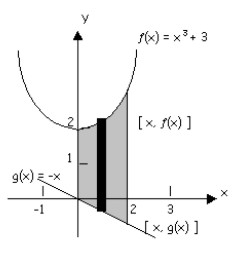


Por tanto decimos que a = 6 y b = - 1 y el área de la región bajo las funciones será:
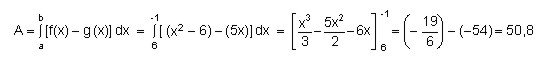
Otros ejemplos de fórmulas que calculan el área de una región según su gráfica son:

4.1.18.1 Ejemplo de aplicación

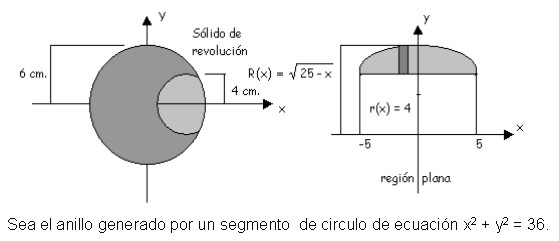
Problema
Un mecánico hace un agujero de 4 cm de radio en el centro de una esfera de 6 cm. de radio. ¿Cuál es el volumen del anillo que resulta?