UNIDAD 7
7. Relatividad
La teoría de la relatividad nace con el fin de complementar el trabajo que se había realizado hasta el momento, el cual se puede sintetizar en la mecánica newtoniana que presentaba problemas cuando se consideraban velocidades altas cercanas a la velocidad de la luz. En lo que trabajó Albert Einstein, quien logró publicar la teoría especial de la relatividad en el año de 1905, cuando tenía 26 años. En este año en el cual plantea la teoría especial de la relatividad (la cual desarrollaremos) y años más tarde publica la teoría general de la relatividad (que no se tratará porque el desarrollo matemático es demasiado complejo y utiliza métodos aun no estudiados).
La teoría de la relatividad se basa en el planteamiento de dos postulados que son: Las leyes físicas son aplicables y serán las mismas en cualquier sistema de referencia inercial.
![]()
Para comenzar con el estudio de las cualidades que se presentan cuando un cuerpo se desplaza con una velocidad cercana a la de la luz, iniciaremos con los sistemas de referencia inerciales para lo cual se ha llamado al medio, lugar, sitio o espacio en donde se caracteriza, porque si presenta movimiento tiene que ser uniforme sin la presencia de cualquier tipo de aceleración.
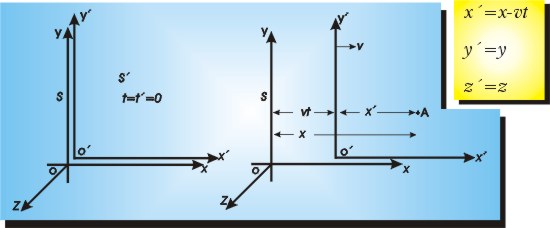

En este caso el bus constituye un SRI, y el observador será otro SRI que lo cual será analizado más adelante. Por ahora lo que nos interesa es lograr relacionar las características de los sistemas de referencia 1 y 2, para tal fin se debe considerar que los tiempos t y t' deben ser iguales entre si a cero, luego:
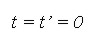
Esto se puede realizar afirmando que los orígenes de los dos sistemas coinciden, como consecuencia de esto se obtiene:

Estas tres expresiones son conocidas con el nombre de transformaciones de Galileo, las cuales se pueden aplicar a eventos que presenten movimiento en los ejes Y o Z.
De estas transformaciones se pueden calcular otras variaciones de la velocidad en forma sencilla y consiste en dividirlas miembro a miembro por t, luego:
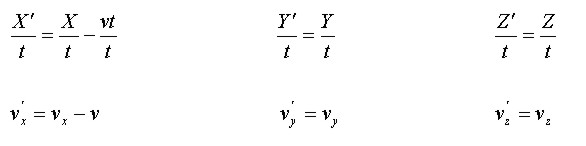
Las últimas expresiones son las transformaciones de velocidades, las cuales tienen problemas de acuerdo con el segundo postulado, ya que éste contradice las transformaciones de Galileo. Por medio de experimentos se ha demostrado que la luz se desplaza a velocidad constante en cualquier dirección sin importar el sistema de referencia inercial.
Analizando el primer postulado nos afirma que podemos dar con seguridad las características de un sistema con referencia a otro, pero no se puede asegurar lo mismo de un único sistema como tal. Como ejemplo consideremos el hecho en que una persona se desplaza en un auto, tal persona no puede asegurar que se encuentra en movimiento, sino toma otro sistema de referencia como pueden ser las personas que se encuentran fuera, puesto que para ellas si estará en movimiento, pero con relación a una persona que se encuentre dentro del auto no se moverá.
Se dice que dos eventos son simultáneos si se producen en un determinado tiempo, el cual debe ser igual para los dos. Para tal fin, los relojes deben estar sincronizados, en donde se debe cumplir que el tiempo que tarda un haz de luz de ir de un reloj a otro debe ser exactamente igual al tiempo que tarda en la venida. La definición de Einstein para la simultaneidad es que dos eventos que se producen en dos puntos 1 y 2 se consideran simultáneos si una persona que se encuentra en la mitad de 1y 2 observa los eventos en un tiempo igual desde que ocurrieron hasta que los observa. Como puede ser que dos linternas retiradas se enciendan, de tal manera que el observador debe ver la luz al mismo tiempo.
Teoría especial de la relatividad. La cual se sustenta en el segundo postulado, para que sea totalmente válido, Einstein tuvo que replantear las transformaciones de Galileo para que sean válidas en diferentes sistemas de referencia inerciales. Para lo cual, afirmó que el espacio y el tiempo variaban de un sistema a otro, planteando lo que se conoce con el nombre de relación espacio-tiempo, y definió un factor g por medio del cual se pueden encontrar expresiones relativistas a partir de las clásicas en donde:
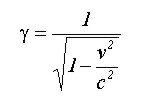
De tal manera que para la posición relativista en X y el tiempo t serán:
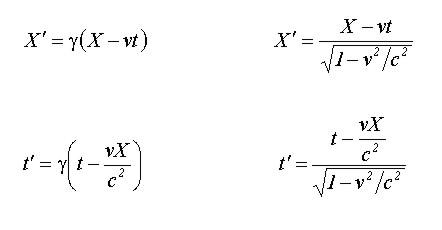
De acuerdo con estas nuevas transformaciones debemos replantear también las transformaciones para la velocidad, para tal hecho, consideremos que una partícula se desplaza en un sistema de referencia inercial con una velocidad v, la cual debemos calcular desde otro sistema de referencia en el cual se observara una velocidad V de tal manera que:
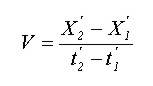
En donde reemplazamos las posiciones y los tiempos respectivos, obteniendo:

Replanteando la anterior expresión se obtiene:

La anterior expresión se conoce con el nombre de transformación de Lorentz, puesto que fue el primero en obtener tal resultado, el cual fue sustentado plenamente por Einstein.
Si la masa de un cuerpo es medida en dos sistemas de referencia inerciales, uno en movimiento con respecto al otro, se encontrará que no son iguales pues la masa varía directamente proporcional a la velocidad de la siguiente manera:
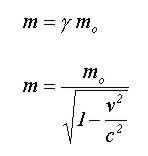

Si consideramos dos sistemas de referencia inercial, uno en movimiento con respecto al otro, durante un intervalo de tiempo, tal tiempo no será igual para los dos sistemas, puesto que de acuerdo a lo planteado por Einstein, existe una dilatación de tiempo cuando se presentan desplazamientos cercanos a la velocidad de la luz. De tal manera que, si t es el intervalo de tiempo en un sistema inercial t, es el tiempo en un sistema de referencia que se mueve a una velocidad v con relación al primer sistema.

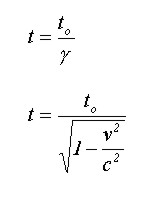


De acuerdo a esto se tienen dos sistemas de referencias una en movimiento OVNI con el otro la velocidad del OVNI en relación para el tripulante es:
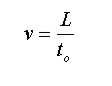
Y la velocidad del OVNI respecto al observador terrícola será:
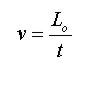
Luego de la primera expresión se tiene que:
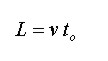
En donde se reemplaza el valor de v obteniendo:
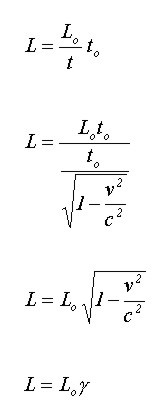
Esto demuestra que la distancia L medida por el observador en movimiento será menor a la medida por el observador estático.
